206 Rationelle Konstruktion
Aus Pattern Language Wiki
... dieses Muster ergänzt das vorige - DIE KONSTRUKTION FOLGT DEN SOZIALEN RÄUMEN (205). Während jenes die Beziehung zwischen den sozialen Räumen und der Konstruktion bestimmt, befasst sich dieses mit der Konstruktion als Gegenstand der Statik. Wie man sehen wird, ist es mit DIE KONSTRUKTION FOLGT DEN SOZIALEN RÄUMEN (205) vereinbar und trägt zu dessen Entstehung bei.
Manche Gebäude sind aus Stützen und Balken konstruiert; andere haben tragende Wände und Deckentplatten; andere sind Gewölbekonstruktionen, Kuppeln oder Zelte. Aber welche davon, oder welche Zusammensetzung aus diesen, ist wirklich die rationellste? Wie kann man Material am besten in einem Gebäude verteilen, um den Raum mit der geringstmöglichen Menge an Material fest und gut zu umschließen?
Techniker pflegen zu sagen, daß es auf diese Frage keine Antwort gibt. Nach gegenwärtiger Ingenieurbaupraxis muß man zunächst eine willkürliche Wahl aus den möglichen Grundsystemen treffen - und kann. erst dann Theorie und Berechnung anwenden, um die Größe der Teile innerhalb des gewählten Systems zu bemessen. Aber die grundlegende Wahl selbst kann - zumindest nach der herrschenden Lehre - nicht durch die Theorie getroffen werden.
Jedem forschenden Geist muss das ganz unwahrscheinlich vorkommen. Dass so eine grundlegende Wahl wie die zwischen Stützen- und Balkensystemen, tragenden Wandsystemen und Gewölbesystemen völlig im Bereich der Laune liegen sollte und dass die mögliche Unzahl zusammengesetzter Systeme, die zwischen diesen Archetypen liegen, nicht einmal in Betracht gezogen werden könne -, hängt wohl mehr mit dem Zustand verfügbarer Theorie zusammen als mit irgendeiner grundlegenden Einsicht.
Wie wir gleich zu zeigen versuchen werden, ist tatsächlich die archetypische, beste Lösung des Problems der rationellen Konstruktion eines Bauwerks eine, die zwischen den drei bekanntesten Archetypen liegt. Es ist ein System tragender Wände, in geringen Abständen durch verdickte Aussteifungen wie Pfeiler unterstützt, mit einem gewölbten Deckensystem.
Wir werden die Merkmale der rationellsten Konstruktion in drei Schritten herleiten. Zunächst werden wir den dreidimensionalen Charakter eines typischen Systems von Räumen und Volumina in einem Gebäude bestimmen. Sodann werden wir eine rationelle Konstruktion definieren als die kleinste, billigste Menge haltbaren Materiäls, lediglich zwischen den Räumen angeordnet, die ihre eigenen und die in den Räumen entstehenden Lasten tragen kann. Zuletzt werden wir die Einzelheiten einer rationellen Konstruktion entwickeln. Für eine ähnliche Erörterung siehe Christopher Alexander, „An attempt to derive the nature of a human building system from first principles", in Edward Allen, The Responsive House, M.I.T. Press, 1974.
I. Die dreidimensionalen Merkmale eines typischen Gebäudes, Die dreidimensionalen Merkmale eines typischen Gebäudes, das ausschließlich auf den sozialen Räumen und den Raumeigenschaften beruht.
Um diese von Grund auf zu entwickeln, betrachten wir zuerst die typische Form von Räumen - siehe FORM DES INNENRAUMS (191) - und leiten dann daraus die rationellste Konstruktion für ein Gebäude ab, das aus solchen Räumen zusammengesetzt ist:
- Jeder Raum wird im Grundriss durch Segmente gebildet, die - obwohl sie nicht vollkommen gerade sein müssen - im wesentlichen gerade Linien darstellen.
- Die Deckenhöhen von Räumen variieren je nach deren sozialer Funktion. Grob gesprochen, variieren die Deckenhöhen mit den Bodenflächen - große Räume haben höhere Decken, kleine niedrigere - VERSCHIEDENE RAUMHÖHEN (190).
- Die Raumkanten sind im wesentlichen vertikal bis zur Kopfhöhe - d.h. bis etwa 1,80 m. Oberhalb der Kopfhöhe kann die Raumbegrenzung weiter nach innen verlaufen. Die oberen Kanten zwischen Wand und Decke eines normalen Raumes dienen keinem Zweck. Es ist also nicht sinnvoll, sie als wesentlichen Teil des Raumes zu betrachten.
- Jeder Raum hat einen horizontalen Boden.
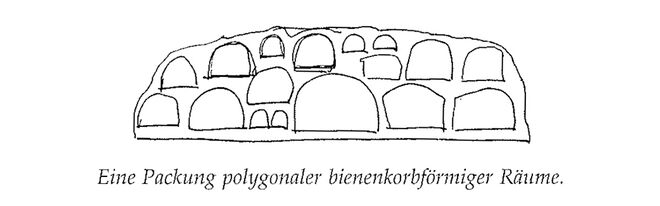
- Ein Gebäude ist also eine Packung polygonaler Räume, in der jedes Polygon im Querschnitt die Form eines Bienenkorbs hat — und eine Höhe, die entsprechend seiner Größe variiert.
Dem Prinzip DIE KONSTRUKTION FOLGT DEN SOZIALEN RÄUMEN (205) folgend, können wir voraussetzen, dass diese dreidimensionale Anordnung von Räumen intakt bleiben muss und nicht durch Konstruktionselemente unterbrochen werden darf. Demnach darf in einer rationellen Konstruktion das Material nur die Zwischenräume einnehmen.
Die primitivste dieser möglichen Konstruktionen können wir uns durch die Vorstellung eines einfachen Vorganges veranschaulichen. Nehmen wir einen Wachsklumpen für jeden im Gebäude vorkommenden Raum und entwerfen wir eine dreidimensionale Anordnung dieser Wachsklumpen, indem wir zwischen aneinander liegenden Klumpen Abstände lassen. Dann nehmen wir eine verallgemeinerte „Konstruktionsflüssigkeit" und gießen sie über diese Anordnung von Klumpen, sodass das Ganze vollständig bedeckt ist und alle Abstände ausfüllt. Wenn die Flüssigkeit erhärtet ist, lösen wir die Wachsklumpen, die die Räume darstellen, auf. Was übrig bleibt ist die Konstruktion des Gebäudes in ihrer allgemeinsten Form.
II. Die rationellste Konstruktion für ein gegebenes System von Räumen.
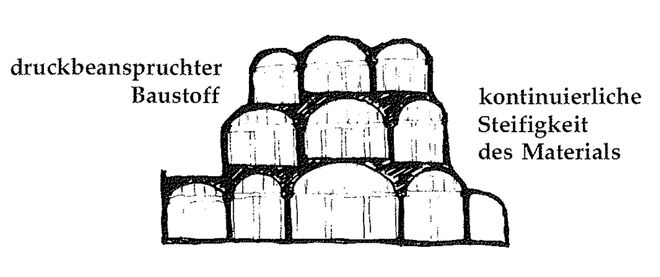
Natürlich ist die gedachte Konstruktion aus Konstruktionsflüssigkeit unrealistisch. Übrigens ist sie eher unrationell: sie würde, wenn sie wirklich ausgeführt würde, viel Material verbrauchen. Wir müssen nach einer dieser Vorstellung ähnlichen Konstruktion suchen, die hingegen mit der geringsten Menge von Material auskommt. Wie wir sehen werden, muss diese rationellste Konstruktion eine druckbeanspruchte Konstruktion sein, in der Biegung und Zug auf ein Minimum reduziert sind, und eine steife Konstruktion, in der alle Teile fest verbunden sind, sodass jeder Teil zumindest einen Teil der Spannungen übernimmt, die durch irgendeinen Lastfall entstehen.
- Eine druckbeanspruchte Konstruktion. In einer rationellen Konstruktion wollen wir, dass jedes Gramm Material voll beansprucht wird. Genauer formuliert, wollen wir, dass die Spannungen im Material so verteilt sind, dass in jedem Kubikzentimeter dieselben Spannungen auftreten. Das ist bei einem einfachen Holzbalken z. B. nicht der Fall. Die größten Spannungen treten am oberen und unteren Rand des Balkens auf; die mittlere Zone des Balkens hat nur geringe Spannungen, weil sich dort im Verhältnis zur Spannungsverteilung zu viel Material befindet. Ganz allgemein kann man sagen, dass biegebeanspruchte Teile immer ungleiche Spannungsverteilungen aufweisen und dass man deshalb die Spannungen nur dann gleichmäßig im Material verteilen kann, wenn die Konstruktion völlig frei von Biegebeanspruchungen ist. Kurz gesagt also, eine perfekt rationelle Konstruktion muss biegungsfrei sein. Es gibt zwei mögliche Konstruktionssysteme, die Biegung überhaupt vermeiden: reine Zugkonstruktionen und reine Druckkonstruktionen. Obwohl zugbeanspruchte Konstruktionen theoretisch interessant und in manchen Fällen für spezielle Zwecke geeignet sind, werden sie durch die Erwägungen, die in GUTE BAUSTOFFE (207) beschrieben sind, überwiegend ausgeschlossen, und zwar, weil auf Zug beanspruchbare Baustoffe schwer erhältlich und teuer sind, während fast alle Materialien Druck aufnehmen können. Man denke insbesondere daran, dass sowohl Holz als auch Stahl, die beiden wichtigsten Baustoffe für Zugbeanspruchung, beide knapp sind und aus ökologischen Gründen nicht mehr in großen Mengen verwendet werden können — siehe auch dazu GUTE BAUSTOFFE (207).
- Eine steife Konstruktion. In einer rationellen Konstruktion gilt nicht nur, dass die einzelnen Teile unter der Last gleiche Spannungsverteilungen haben. Es gilt auch, dass die Konstruktion als ein Ganzes wirkt. Nehmen wir z. B. einen Korb: Die einzelnen Ruten des Korbes sind schwach; für sich kann keine viel Last aufnehmen. Der Korb ist aber so geschickt gemacht, dass alle Ruten selbst bei kleinster Last zusammenwirken. Wenn man an einem Teil des Korbes mit dem Finger drückt, wirken alle Ruten — auch die weiter entfernten — zusammen, um der Last standzuhalten. Und natürlich muss, da die Konstruktion als Ganzes die Last aufnimmt, kein Teil für sich sehr stark sein. Dieses Prinzip ist in einer Konstruktion wie einem Gebäude, das einer breiten Skala verschiedener Lastbedingungen ausgesetzt ist, besonders wichtig. Einmal weht der Wind sehr stark aus einer Richtung; dann wieder wird das Gebäude von einem Erdbeben gerüttelt; im Lauf der Jahre gibt es durch ungleichmäßige Setzung eine Umverteilung der ruhenden Lasten, weil manche Fundamente tiefer sinken als andere; und natürlich bewegen sich Menschen und Möbel im Gebäude ständig während der gesamten Lebensdauer. Wenn jeder Teil für sich stark genug sein sollte, um seine mögliche Höchstbelastung aufnehmen zu können, müsste er riesige Ausmaße haben. Aber wenn das Gebäude steif ist wie ein Korb, sodass jeder Teil beim Tragen der kleinsten Last mitwirkt, dann stellt natürlich die Unvorhersehbarkeit der Lasten kein Problem dar. Die Teile können schwach sein, weil die Steifheit des Gebäudes auch die größten Lasten auf die Teile als Ganzes verteilt und das Gebäude ihnen als Ganzes standhält. Die Steifheit eines Gebäudes hängt von seinen Verbindungen ab: wirkliche Steifheit des Materials und der Form. Es ist sehr schwer, fast unmöglich, zwischen verschiedenen Baustoffen steife Verbindungen herzustellen, durch die Kräfte ebenso wirksam übertragen werden wie in gleichem Material; deshalb ist es wichtig, dass das Gebäude aus einem einzigen Baustoff gemacht ist, der von Teil zu Teil durchgehend verbunden ist. Die Form der Verbindungen zwischen den Elementen ist ebenso wichtig. Rechte Winkel tendieren zur Unsteifigkeit: Kräfte können im Gebäude nur verteilt werden, wenn es diagonale Aussteifungen gibt, wo Wände und Decken, Wände und Wände, Stützen und Balken zusammenkommen.
III. Die Einzelheiten einer rationellen Konstruktion.
Wenn wir also annehmen, dass ein rationelles Gebäude einerseits eine druckbeanspruchte und andererseits eine steife Konstruktion haben muss, können wir die wichtigsten morphologischen Eigenschaften seiner Struktur in direkter Schlussfolgerung ableiten.
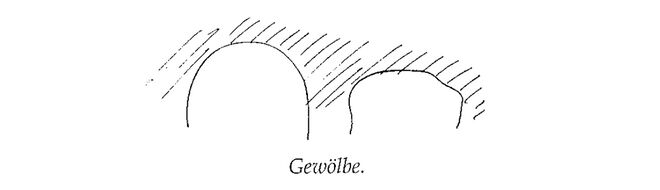
- Die Decken über allen Räumen müssen gewölbt sein. Dies kann man direkt folgern. Die Kuppel- oder Gewölbeform ist die einzige, die mit reinem Druck arbeitet. Decken und Dächer können nur steif mit den Wänden verbunden sein, wenn sie sich an den Rändern nach unten krümmen, und die Gestalt sozialer Räume legt es direkt nahe — da der dreieckige Raum zwischen Wand und Decke keinen sinnvollen Zweck erfüllt, ist er ein gegebener Ort für Konstruktionsmaterial.
- Alle Wände müssen tragend sein. Jede nicht tragende Scheidewand widerspricht offensichtlich dem Prinzip der Kontinuität, das besagt, dass jedes Teilchen des Gebäudes an der Lastabtragung mitwirkt. Außerdem brauchen Stützen mit nicht tragenden Wänden dazwischen Sicherheit gegen Ausknicken. Die Wand liefert diese von selbst; die Steifigkeit von Boden, Wänden und Decke kann nur durch die Wirkung einer alles verbindenden Wand entstehen.
- Wände müssen in Abständen entlang ihrer Länge durch Pfeilervorlagen versteift werden. Eine Wand aus einer gegebenen Menge von Baustoff ist dann am effizientesten, wenn das Material ungleichmäßig verteilt wird und vertikale Rippen bildet. Eine solche Wand hat den wirksamsten Widerstand gegen Knicken — tatsächlich ist bei den meisten Wandstärken eine solche Aussteifung erforderlich, um die zulässige Druckspannung ausnützen zu können - siehe VERTEILUNG DER PFEILER (213). Sie hilft auch bei der Aufnahme horizontaler Kräfte, weil die Versteifungen gegen sie wie Balken wirken.
- Verbindungen zwischen Wänden und Decken und zwischen Wänden und Wänden müssen durch zusätzliches Material in Form einer Hohlkehle entlang der Kante verstärkt werden. Verbindungen sind Schwachpunkte der Steifigkeit, und rechtwinkelige Verbindungen sind am schwächsten. Wir wissen aber aus DIE FORM DES INNENRAUMS (191), dass sich annähernd rechte Winkel nicht vermeiden lassen, wo Wände auf Wände treffen; und natürlich muss es annähernd rechte Winkel geben, wo Wände und Decken zusammentreffen. Um die schädliche Wirkung des rechten Winkels zu verringern, muss man den Winkel mit Material „füllen". Dieses Prinzip wird unter SICHTBARE AUSSTEIFUNG (227) besprochen.
- Öffnungen in Wänden müssen verstärkte Rahmen und Abrundungen in den oberen Ecken haben. Dies lässt sich direkt aus dem Prinzip der kontinuierlichen Steifigkeit ableiten und wird in GERAHMTE ÖFFNUNGEN (225) ausführlich besprochen.
Daraus folgt:
Betrachte das Gebäude als ein aus einer kontinuierlichen Masse von druckbeanspruchtem Baustoff bestehendes Gebilde. Bezüglich seiner Geometrie betrachte es als ein dreidimensionales System von gewölbten Einzelräumen, die meisten davon annähernd rechteckig; mit dünnen tragenden Wänden, die in ihrer Länge in Abständen durch Pfeiler versteift sind, verstärkt in den Verbindungen zwischen Wänden und Wänden und zwischen Wänden und Gewölben und verstärkt rund um die Öffnungen.
Die Anlage der inneren Gewölbe wird behandelt in ANLAGE DER GESCHOSSDECKEN (210) und GEWÖLBTE DECKEN (219); die Anlage der äußeren Gewölbe, die das Dach bilden, wird behandelt in ANORDNUNG DER DÄCHER (209) und GEWÖLBTE DÄCHER (220). Die Anlage der Versteifungen in den Wänden wird behandelt in VERTEILUNG DER PFEILER (213); die Anlage der Verstärkungen an den Schnittpunkten von Wänden wird behandelt in PFEILER IN DEN ECKEN (212); die Verstärkung an der Verbindung zwischen Wänden und Gewölben wird behandelt in RANDBALKEN (217); der Bau der Pfeiler und der Wände wird behandelt in KASTENPFEILER (216) und WANDSCHALEN (218); die Verstärkung von Tür- und Fensterrahmen wird behandelt in GERAHMTE ÖFFNUNGEN (225); und die nicht rechtwinkelige Verbindung zwischen Stützen und Balken in SICHTBARE AUSSTEIFUNG (227)