213 Verteilung der Pfeiler
Aus Pattern Language Wiki
... wenn die Eckpfeiler, die die Räume definieren, platziert sind - PFEILER IN DEN ECKEN (212) -, müssen die Abstände zwischen den Pfeilern mit aussteifenden Zwischenpfeilern überbrückt werden, wie in RATIONELLE KONSTRUKTION (206) verlangt. Das folgende Muster ergibt die Abstände dieser Zwischenpfeiler und führt zur Ausbildung jener Art von Wänden, die in RATIONELLE KONSTRUKTION (206) beschrieben sind. Es trägt auch bei zur Entstehung VERSCHIEDENER RAUMHÖHEN (190).
Wie verhalten sich die Abstände der Nebenpfeiler, die die Wände aussteifen, zur Raumhöhe, zur Anzahl der Geschosse und zur Größe der Räume?
Ganz grob können wir diese Frage auf intuitive Weise beantworten. Wenn wir uns ein Gebäude vorstellen, dessen Wände in Abständen verstärkt sind, sehen wir, dass der Maßstab dieser Aussteifungen in der Nähe des Bodens - in der Zone der größten sozialen Räume und der höchsten Lastbeanspruchungen - am größten, dagegen in der Nähe des Daches - der Zone der kleinsten Räume und der geringsten Lasten - am kleinsten sein muss. Auf die gleiche grobe und anschauliche Art lasst uns die Intuition im Gerippe eines Blattes die feinste Textur am zarten Rand, wo alles am kleinsten ist, und die gröbere, rohere Struktur in der Nähe der größeren Teile erwarten.
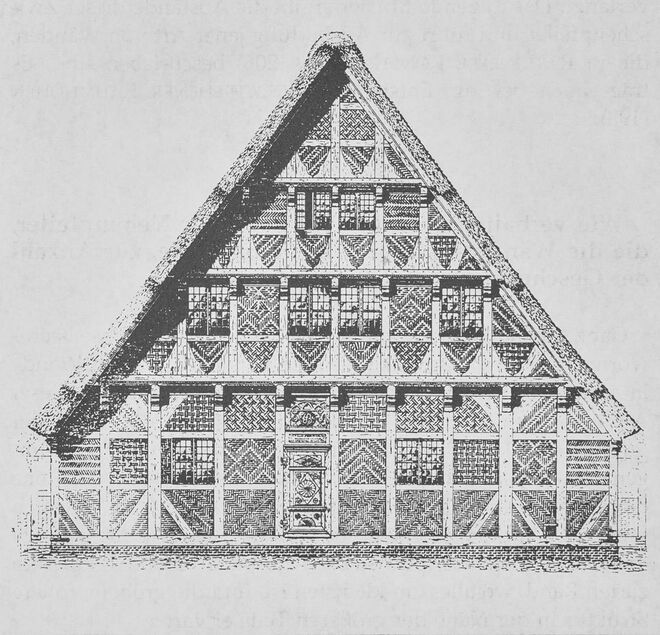
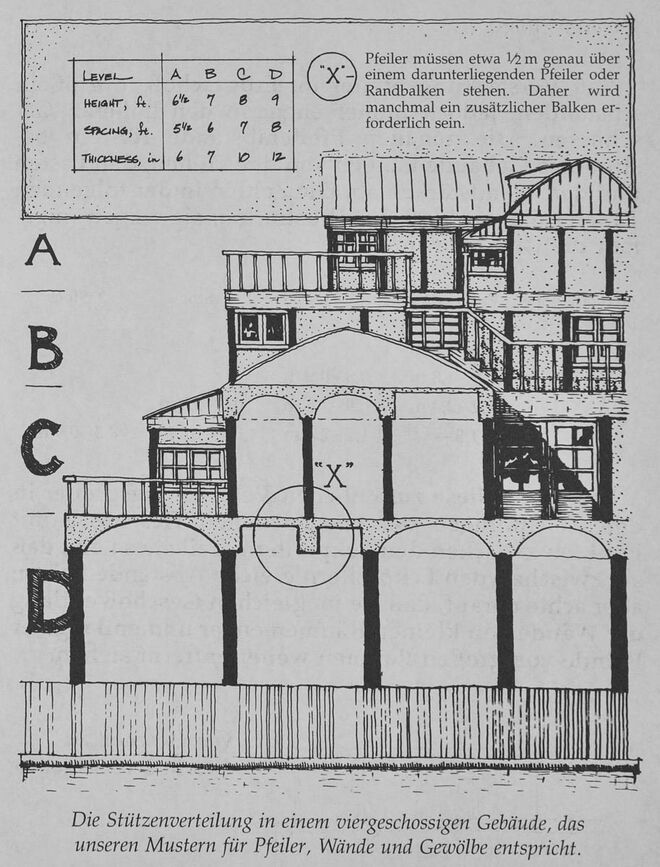
Diese Intuition wird durch viele traditionelle Bauformen bestätigt, wo Pfeiler, Rahmen oder Aussteifungen in der Nähe des Bodens größer und weiter voneinander entfernt sind, weiter oben dagegen zarter und näher beisammen. Das Titelbild dieses Musters zeigt ein Beispiel. Aber welche konstruktive Grundlage hat diese Intuition?
Die Theorie elastischer Platten liefert uns eine formale Erklärung.
Betrachten wir eine dünne unausgesteifte Wand, die eine axiale Last aufnimmt. Weil sie dünn ist, wird diese Wand gewöhnlich durch Ausknicken versagen, bevor sie durch reine Druckbeanspruchung versagt. Das bedeutet, daß das Wandmaterial nicht rationell ausgenützt ist. Sie kann die zufolge ihrer Druckfestigkeit mögliche Last nicht tragen, weil sie zu dünn ist.
Es ist deshalb naheliegend, eine Wand so zu bemessen, dass sie entweder genügend dick oder genügend ausgesteift ist, um Lasten bis zu ihrer vollen Druckfestigkeit ohne Ausknicken aufnehmen zu können. Eine solche Wand, die ihr Material bis an die Grenzen seiner Druckfestigkeit ausnützt, entspricht dann auch den Anforderungen einer RATIONELLEN KONSTRUKTION (206).
Die kritische Größe ist die Schlankheit der Wand: das Verhältnis ihrer Höhe zur ihrer Dicke. Für den einfachen Fall einer unverstärkten Betonwand sagen uns die Vorschriften des American Concrete Institute, dass die Wand einen Wirkungsgrad von 93% hat (d. h. 93% ihrer potentiellen Druckbeanspruchung ohne Ausknicken aufnehmen kann), wenn ihr Schlankheitsgrad 10 oder weniger beträgt. Eine 3 m hohe und 30 cm dicke Wand ist also in diesem Sinn rationell.
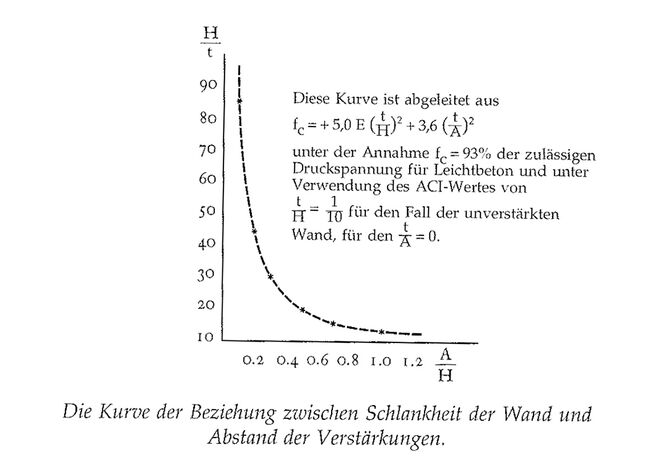
Gehen wir nun weiter in der Theorie elastischer Platten zum Fall einer Wand mit Verstärkungen. Die Gleichung, die zulässige Spannungen mit dem Abstand der Verstärkungen in Beziehung setzt, liefert ähnliche Zahlen für verschiedene Wände mit Verstärkungen. Diese Zahlen sind in der folgenden Kurve wiedergegeben. Z. B. braucht eine Wand mit einem Schlankheitsgrad 20 Verstärkungen in Abständen von 0,5 H (H bedeutet die Wandhöhe), wodurch eine Plattenteilung in der Breite der halben Höhe entsteht. Ganz allgemein braucht offensichtlich eine Wand, je dünner sie im Verhältnis zu ihrer Höhe ist, desto mehr Verstärkungen in ihrer Länge.
In jedem Fall gibt die Kurve den Abstand der Verstärkungen an, der erforderlich ist, damit die Wand mit 93% ihrer Druckfestigkeit wirkt. Abgekürzt können wir sägen, daß eine Wand, die dem Prinzip der RATIONELLEN KONSTRUKTION (206) folgt, entsprechend dieser Kurve verstärkt werden sollte.
Das Kleinerwerden der Pfeilerabstände über die verschiedenen Geschosse folgt direkt aus dieser Kurve. Wir können uns das in der folgenden Weise klar machen: die Wände eines viergeschossigen Gebäudes erhalten Lasten, die etwa im Verhältnis 4: 3 : 2 : 1 stehen (wirklich sehr grob gesprochen). Auf jeden Fall werden die von den Wänden aufgenommenen Lasten weniger und weniger, je höher sie im Gebäude liegen. Wenn alle Wände bis zu ihrer vollen Druckfestigkeit ausgenützt sind, bedeutet dies, dass sie auch immer dünner werden müssen, je höher sie im Gebäude liegen. Wenn wir annehmen, dass alle Wände gleich hoch sind, werden die Wände die vier Geschosse fortschreitend immer größere Schlankheitsgrade haben, daher immer weiter in der Kurve nach links wandern und daher in immer kleineren Abständen verstärkt werden müssen.
Nehmen wir z. B. ein viergeschossiges Gebäude an, mit 2,4 m hohen Wänden in allen Geschossen und Wandstärken von 30 cm, 22,5 cm, 15 cm und 7,5 cm in den vier Geschossen. Die Schlankheitsgrade betragen dann 8, 11, 17 und 33. Wenn wir für diesen Fall die Kurve ablesen, ergeben sich für das Erdgeschoß überhaupt keine Verstärkungen (sie sind unendlich weit voneinander entfernt), im 1. Stock ergeben sich Verstärkungen in Abständen von etwa 2,4 m, im 2. Stock in Abständen von etwa 1,5 m und im obersten Geschoß in Entfernungen von etwa 0,6 m.
In einem anderen Fall mit dünneren Wänden (wegen leichterer Baustoffe und kleinerer Lasten) werden die Abstände geringer sein. Nehmen wir an, die erforderlichen Wandstärken wären 20 cm, 15 cm, 10 cm und 5 cm. Dann betragen die Schlankheitsgrade 12, 16, 24 und 48 und die Verstärkungen müssen enger sitzen als im vorigen Beispiel: in Abständen von 2,7 In im Erdgeschoß, 1,5 m im 1. Stock, 0,9 m im 2. Stock und 0,4 m im obersten.
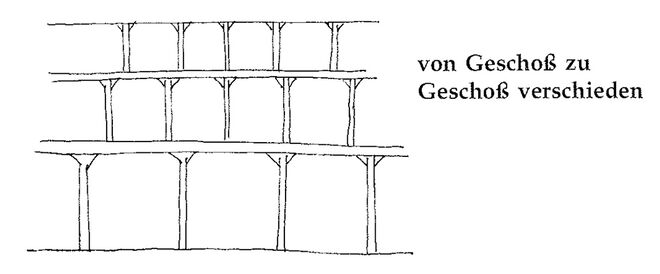
Wie man aus diesen Beispielen ersieht, sind die Unterschiede in den Pfeilerabständen überraschend groß; tatsächlich größer als man intuitiv annehmen würde. Aber die Unterschiede sind so extrem, weil wir in allen Geschossen gleiche Raumhöhen angenommen haben. In Wirklichkeit wird in einem richtig entworfenen Gebäude die Raumhöhe von Geschoß zu Geschoß variieren; und unter dieser Bedingung werden die Unterschiede, wie wir sehen werden, viel vernünftiger. Es gibt zwei Gründe, deretwegen die Raumhöhe von Geschoß zu Geschoß variieren muss: einen sozialen und einen konstruktiven.
In den meisten Gebäuden werden die Räume im Erdgeschoß eher größer sein, weil gemeinschaftliche Räume, Räume in denen man zusammenkommt usw., meist besser in der Nähe des Einganges untergebracht sind, während private und kleinere Räume eher weiter oben, also tiefer im Gebäudeinneren, sein werden. Da die Raumhöhen mit der Größe der sozialen Räume variieren - siehe VERSCHIEDENE RAUMHÖHEN (190) -, bedeutet dies, dass die Raumhöhen im Erdgeschoß größer sind und nach oben kleiner werden. Und das Dachgeschoß hat entweder sehr niedrige Wände oder überhaupt keine - siehe SCHÜTZENDES DACH (117).
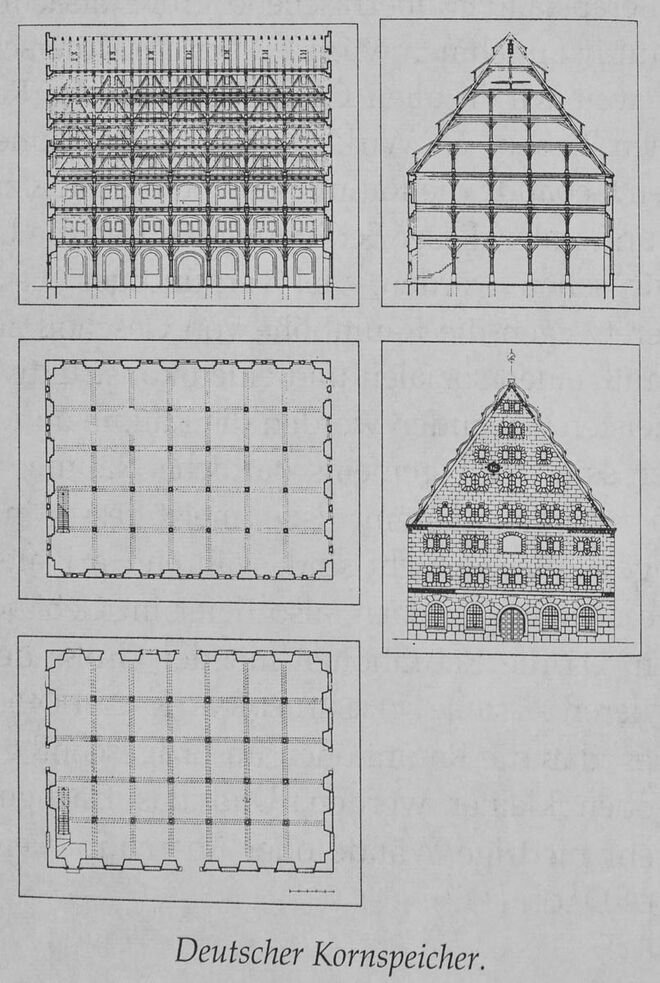
Und dann gibt es eine zweite, rein konstruktive Erklärung dafür, dass die Raumhöhen in den oberen Geschossen niedriger sind. Sie ist in der folgenden Zeichnung eines Kornspeichers enthalten. Nehmen wir an, ein Stützensystem wird rein nach den konstruktiven Anforderungen bemessen. Die Stützen in den höheren Geschossen werden dünner sein, weil sie weniger Last aufnehmen als die in den unteren Geschossen. Aber weil sie dünner sind, haben sie weniger Knickfestigkeit und müssen daher kürzer sein, wenn kein Material verschwendet werden soll. Als Folge davon ergibt sich sogar in einem Kornspeicher, wo es keine sozialen Gründe für verschiedene Raumhöhen gibt, aus rein konstruktiven Überlegungen die Notwendigkeit dicker Stützen und hoher Räume in den unteren und fortschreitend dünnerer Stützen und niedrigerer Räume, je weiter man hinaufkommt.
Zum selben Schluss kommen wir durch Betrachtung unserer Kurve. Wir haben vorher die Kurve verwendet, um festzustellen, dass die Verstärkungen in den oberen Geschossen in kürzeren Abständen stehen müssen, weil die Wände schlanker sind. Wir können die Kurve aber auch benützen, um bei einer gegebenen Belastung den Schlankheitsgrad so niedrig wie möglich zu halten. In den oberen Geschossen, wo die Wände eher dünn sind, sollten wir sie deshalb so niedrig wie möglich machen, um den Schlankheitsgrad niedrig zu halten.
Nehmen wir nun an, die Wände in einem Gebäude wären entsprechend diesen Gedankengängen verschieden hoch. Ein viergeschossiges Gebäude mit einem zusätzlichen Dachgeschoß könnte dann folgende Wandhöhen haben (man berücksichtige, dass der Gewölbescheitel in einem gewölbten Raum größer ist als die Wandhöhe). 2,7 m im Erdgeschoß, 2,1 m im 1. Stock, 1,8 m im 2. Stock und 1,2 m im obersten, wo das schräge Dach an der Traufkante tief herunterkommt. Und nehmen wir weiter an, dass die Wandstärken jeweils 30 cm, 15 cm, 12,5 cm und 7,5 cm betragen. In diesem Fall betragen die Schlankheitsgrade 9, 14, 14, 15. Das Erdgeschoß braucht überhaupt keine Verstärkungen, der 1. Stock braucht sie in Abständen von 1,8 m, der 2. in Abständen von 1,5 m und der letzte in Abständen von 0,9 m. Die folgende Zeichnung zeigt eine ähnliche Verteilung.
Bei der Anwendung dieses Musters auf den Geschoßgrundriss wird man auf eine gewisse Schwierigkeit stoßen. Da die Raumecken vielleicht durch PFEILER IN DEN ECKEN (212) bereits fixiert sind, ist es nicht immer möglich, die Abstände der Verstärkungen in der Wand jedes einzelnen Raumes genau einzuhalten. Natürlich macht das nicht sehr viel aus; die Verstärkungen müssen nur ungefähr richtig sein; die Abstände dürfen ruhig von Raum zu Raum variieren, um sie den Wandmaßen anzupassen. Im großen und ganzen aber muß man versuchen, in kleinen Räumen die Verstärkungen enger und in großen Räumen weiter zu setzen. Wenn man das nicht macht, sieht das Gebäude vielleicht seltsam aus, weil es der konstruktiven Intuition widerspricht.
Nehmen wir zwei Räume im selben Geschoß, der eine zweimal so groß wie der andere. Der größere Raum hat den doppelten Umfang, seine Decke erzeugt aber die vierfache Last; die Wand trägt also eine größere Last pro Längeneinheit. In einer idealen rationellen Konstruktion bedeutet das, dass die Wand dicker sein muss; also wird sie nach den bisherigen Gedankengängen weiter auseinander liegende Verstärkungen brauchen als der kleinere Raum mit weniger Last und dünneren Wänden.
Es ist verständlich, dass eine Baufirma sich kaum die Mühe machen wird, in einem Geschoß von Raum zu Raum die Wandstärken zu variieren. Aber auch wenn die Wand gleichmäßig dick ist, sollten nach unserer Meinung die Verstärkungen der Regel zumindest nicht widersprechen. Wenn der Abstand zwischen Verstärkungen aus Gründen der Anordnung von Raum zu Raum variieren muss, dann sollten die größeren Abstände auf jene Wände entfallen, die die größeren Räume umschließen. Würden die größeren Abstände mit den kleineren Räumen zusammenfallen, würde das Auge getäuscht, und man würde das Gebäude missverstehen.
Eine wichtige Bemerkung. Die ganze vorhergehende Analyse beruht auf der Annahme, dass sich Wände und Verstärkungen wie elastische Platten verhalten. Im großen und ganzen stimmt das; und das beschriebene Phänomen ist dadurch leichter zu erklären. Allerdings verhält sich keine Wand als perfekte elastische Platte, am wenigsten die Art von Leichtbetonwänden, die wir in den übrigen Mustern zur Bauweise propagieren. Wir haben deshalb eine modifizierte Theorie elastischer Platten verwendet, unter Berücksichtigung der Vorschriften des American Concrete Institute, sodass die Zahlen unserer Analyse auf dem Elastizitätsverhalten des Betons beruhen (und innerhalb seiner zulässigen Zug- und Druckbeanspruchungen bleiben). Allerdings werden ändere Faktoren eintreten, wenn die Platte durch Rissbildung den elastischen Bereich verlässt, was in einer Betonkonstruktion praktisch mit Sicherheit eintritt. Wir weisen den Leser deshalb eindringlich darauf hin, dass die faktischen Zahlen unserer Analyse bloß der Illustration dienen. Sie stellen das generelle mathematische Verhalten eines solchen Systems dar, aber sie sind keine zuverlässigen Eingaben für konstruktive Berechnungen.
Daraus folgt:
Bau Verstärkungspfeiler im Erdgeschoß in größten Abständen, jedoch immer enger in den höheren Geschossen. Die genauen Pfeilerabstände für ein bestimmtes Gebäude hängen von den Höhen, den Lasten und den Wandstärken ab. Die Zahlen in der folgenden Tabelle dienen bloß der Illustration; sie zeigen ungefähr die Größenordnungen.
| Gebäudehöhe in Geschossen | Erdgeschoss | 1. Stock | 2. Stock | 3. Stock |
| 1 | 0,6 - 1,5 m | |||
| 2 | 0,9 - 1,8 m | 0,3 - 0,9 m | ||
| 3 | 1,2 - 2,4 m | 0,9 - 1,8 m | 0,3 - 0,9 m | |
| 4 | 1,5 - ∞ | 1,2 - 2,4 m | 0,9 - 1,8 m | 0,3 - 0,9 m |
Bezeichne diese zusätzlichen Verstärkungspfeiler in den Zeichnungen der verschiedenen Geschosse mit Punkten zwischen den Eckpfeilern. Teil sie so ein, dass sie zwischen den Eckpfeilern gleiche Abstände haben aber achte darauf, dass sie im gleichen Geschoß entlang der Wände von kleinen Räumen enger und entlang der Wände von großen Räumen weiter entfernt stehen.
In Übereinstimmung mit VERSCHIEDENEN RAUMHÖHEN (190) mach Wände und Pfeiler zunehmend niedriger, je höher sie im Gebäude liegen, damit die Schlankheitsgrade niedrig bleiben. Variiere Wand- und Pfeilerstärken je nach der Höhenlage — siehe WANDSCHALEN (218). Unsere Berechnungen für ein typisches Leichtbetongebäude, wie wir es erörtert haben, ergeben folgende Größenordnungen für Wandstärken: im obersten Geschoß 5 cm, im Geschoß unter dem obersten 7,5 cm, im dritten von oben 10 cm, im vierten von oben (bei vier Geschossen das Erdgeschoß) 12,5 cm. Natürlich ändern sich diese Zahlen für andere Belastungen oder für andere Baustoffe, aber sie zeigen den Spielraum, der zu erwarten ist.
Pfeilerstärken müssen proportional zu den Wandstärken sein, sodass die dünnsten Wände auch die dünnsten Pfeiler haben. Wenn sie sehr dünn sind, genügt vielleicht eine zusätzliche Brett- oder Materialstärke zusätzlich auf der Außenhaut, die die Wandmembran bildet — siehe WANDSCHALEN (218). Bei dicken Wänden werden es volle Pfeiler sein müssen, doppelt so stark wie die Wand und etwa quadratisch im Querschnitt, und zwar so ausgebildet, dass sie zusammen mit den Wänden betoniert werden können — KASTENPFEILER (216)